Tema 1. Introducción

La fontanería es una profesión en la que los operarios deben tener conocimientos de diferentes disciplinas, entre las que podemos encontrar las matemáticas y la física de fluidos. Para ello, en este primer tema de introducción, vamos a estudiar los principios básicos de matemáticas y física aplicados a la fontanería.

PUNTO 1. MATEMÁTICAS BÁSICAS APLICADAS A LA FONTANERÍA

Los conocimientos sobre matemáticas son indispensables para que el propio fontanero pueda realizar cálculos como la cantidad de tubos a utilizar, diámetros de estos tubos, así como diferentes cálculos de secciones y volúmenes.

Lo primero que se debe conocer es la diferencia entre un número entero y un número decimal. Los números enteros son los que se utilizan para designar elementos que no pueden ser divididos; por ejemplo, si estamos hablando de contabilizar el número de vehículos que hay aparcados en una calle, este cómputo siempre será un número entero, ya que nunca habrá medio coche.

En cambio, los números decimales se utilizan para elementos que sí se pueden fraccionar; por ejemplo, si en este caso estamos hablando de pasteles, sí que podremos coger sólo una porción de estos. Los números decimales se dividen en dos partes, una parte entera y otra parte decimal, separados entre sí por una coma. La parte decimal es la que define la fracción de un elemento que ha sido dividido. De esta forma los números decimales son equivalentes a una fracción, la de dividir un elemento en diferentes partes.

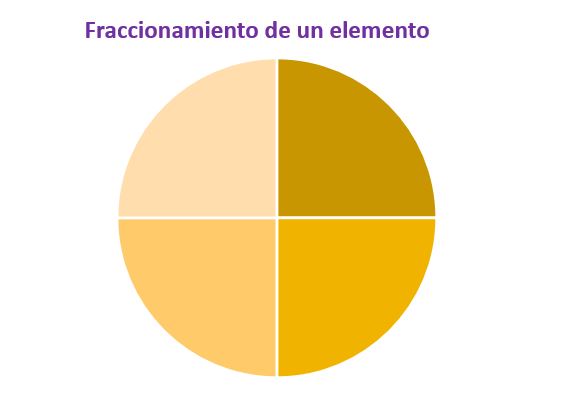
                                3/4 = 0.75

En la figura anterior vemos como el elemento ha sido dividido en cuatro partes iguales, de estas cuatro partes han sido seleccionadas sólo tres, por lo que la fracción correspondiente es 3/4. Sí se realiza la división, el número decimal que se obtienen es 0.75, donde el cero es la parte entera y el 75 es la parte decimal.

1.1. Las superficies

Es muy común en la fontanería que sea necesario realizar cálculos de superficies. Cada forma geométrica tiene una fórmula específica para el cálculo de su superficie. Sin embargo, como en fontanería las más habituales son el rectángulo y la circunferencia, únicamente vamos a ver cómo realizar el cálculo de estas superficies:

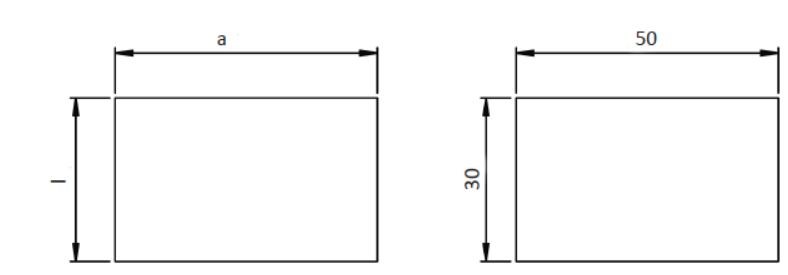
                       Superficie de un rectángulo

La superficie de un rectángulo se calcula como el largo por el ancho. No hay que olvidar, que las unidades de ambas medidas deben ser las mismas, siendo el metro la medida de longitud del sistema internacional. La fórmula para el cálculo de esta superficie será: 

S _rectángulo = l · a

En el ejemplo de la figura anterior, el cálculo de la superficie es:

S _rectángulo = 30 · 50 = 1500 m²

Por otro lado, la forma de calcular la superficie de una circunferencia difiere de la anterior.

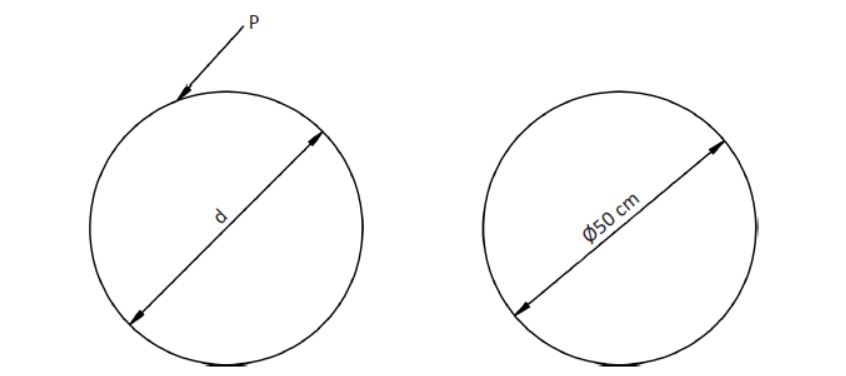
                                    Superficie de una circunferencia

Antes de estudiar la fórmula de cálculo de la superficie, se deben definir una serie de parámetros importantes.

• Diámetro (d o Φ). Es la línea que une dos puntos de una circunferencia y que pasa por su centro.
• Radio (r). Es el valor correspondiente a la mitad del diámetro, por lo que es la línea que une un punto de la circunferencia con su centro. Se representa por la letra r.
• Perímetro (p). Equivale a la longitud de la línea de la circunferencia.
• Pi (π). El número PI es una constante y equivale a 3.14.

Pasamos al cálculo de la superficie de una circunferencia. Para ello utilizaremos la ecuación:

                  r = ^d/₂

                 S _{circunferencia} = π · r²

Con los datos de la figura anterior, realizamos los diferentes cálculos:

                 r = ⁵⁰/₂ = 25 cm

                S _{circunferencia} = 3.14 · (25)² = 1962.5 cm²

A parte del cálculo de la superficie, también podemos realizar el del perímetro:

                P = π · 2 · r = 3.14 · 2 · 25 =157 cm

Pero en fontanería encontramos un problema añadido. El operario puede medir una tubería, pero lo que mide es la parte exterior y con esta medida no se tiene un valor real de la superficie por la que pasa el agua debido al espesor de la propia tubería.

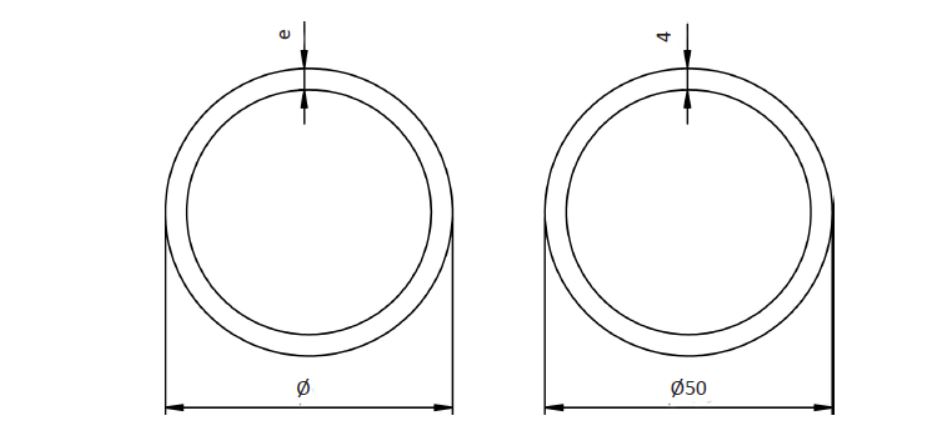
En este caso lo primero que se debe hacer es calcular el diámetro interior como:

                          d _interior = d _exterior – 2 · e

                          d _interior = 50 – 2 · 4 = 42 cm

Ahora ya se puede calcular la superficie interior de la tubería:

                          r = ⁴²/₂= 21 cm

                          S _{circunferencia interior} = 3.14 · (21)² = 1387.7 cm²

Asimismo, es importante conocer también el cálculo del área de un triángulo, ya que esto nos servirá para poder calcular superficies complejas. La superficie de un triángulo se calcula como el producto de la base por su altura dividido entre dos.

 

                     

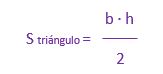
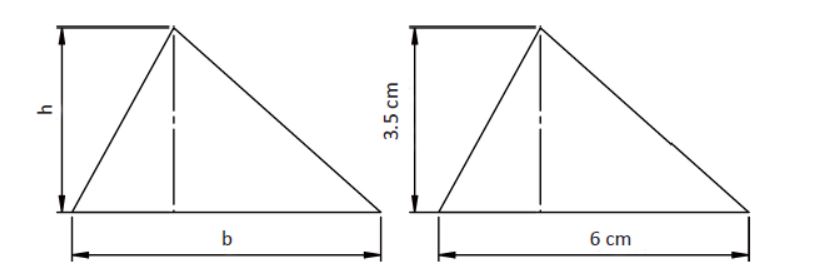
                                      Superficie de un triángulo

Si realizamos el cálculo con los datos de la figura anterior obtenemos la siguiente superficie:

                           

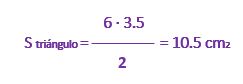
1.2. Volúmenes

Al igual que con la superficie, el profesión en la fontanería también deberá saber calcular ciertos volúmenes. En este caso los volúmenes más importantes que deberemos saber calcular serán el de un prisma de base rectangular, el de un cilindro y el de una esfera. Un prisma de base rectangular no es más que un rectángulo, el cual tiene cierta profundidad. La fórmula utilizada para el cálculo de dicho volumen será siguiente:

                      V _rectangular = a · b · c

 

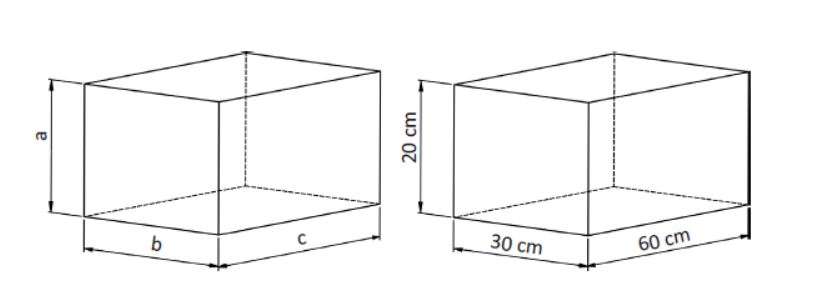
                    Volumen de prisma de base rectangular

Si aplicamos los valores dados por la figura anterior obtenemos el siguiente volumen:

                   V _rectangular = 20 · 30 · 60 = 36000 cm³

Pasamos al cálculo del volumen de un cilindro. Un cilindro es una circunferencia a la que se le ha dado profundidad. Para el cálculo de su volumen utilizaremos la siguiente fórmula:

                   V_cilindro = π · r² · h

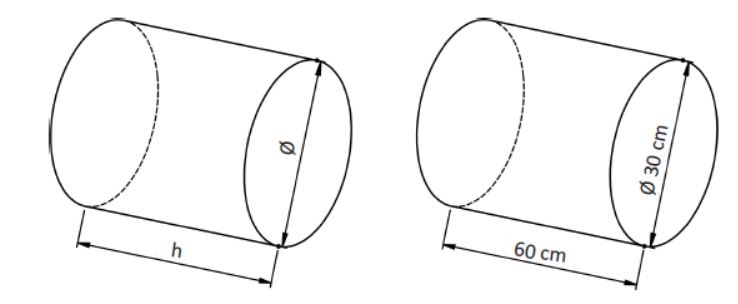
                       Volumen de un cilindro

Realizamos el cálculo utilizando los valores del ejemplo de la figura anterior, teniendo en cuenta que siempre el radio será igual a la mitad del diámetro.

               V _cilindro = 3.14 · 15² · 60 = 42390 cm³

El último caso a estudiar sería el cálculo del volumen de una esfera. Este cálculo se realizará mediante la siguiente ecuación:

                        V_esfera = ₄/₃ · π · r₃

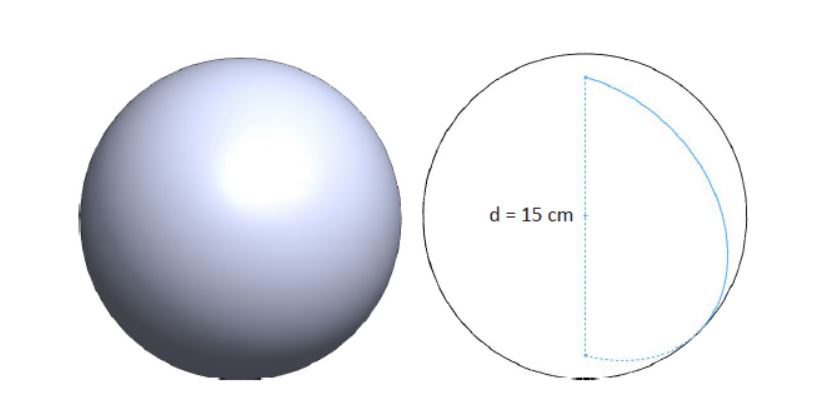
                              Volumen de una esfera

                     V_esfera = ⁴/₃ · 3.14 · (7.5)³ = 1766.25 cm³

1.3. El teorema de Pitágoras

El teorema de Pitágoras relaciona los lados de un triángulo rectángulo. Para poder aplicarlo, debemos definir previamente que es un triángulo rectángulo. Estos triángulos son aquellos que tienen dos lados perpendiculares, es decir, que forman un ángulo de 90° como el que muestra la figura:

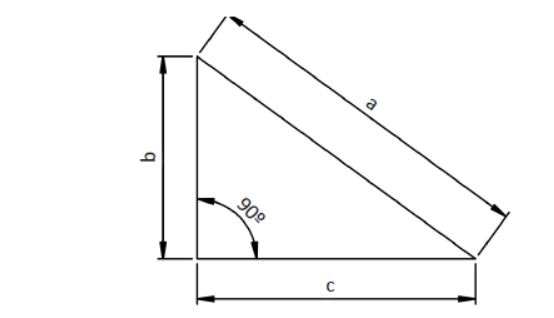
                       Representación de un triángulo rectángulo

En la figura anterior se muestran los diferentes lados del triángulo que reciben los siguientes nombres:

• Hipotenusa (a). Es el lado opuesto al ángulo recto.
• Cateto (b y c). Son los lados menores del triángulo.

La ecuación que define el teorema de Pitágoras es:

                                  a² = b² + c² 

Mediante esta ecuación se puede calcular uno de los lados del triángulo rectángulo sabiendo los otros dos. Es muy utilizada para calcular alturas y longitudes. Vamos a ver un ejemplo práctico de esta teoría. Imaginemos que deseamos calcular la altura que se alcanza al apoyar una escalera de cinco metros sobre una pared, estando la parte inferior de esta escalera situada a 1.5 metros de la pared.

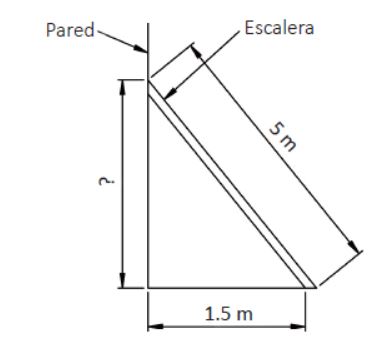
                               Ejemplo práctico

Vemos que estamos frente a un triángulo rectángulo, por lo cual podemos aplicar el teorema de Pitágoras:

a² = b² + c²

5² = b² + 1.5²

Altura alcanzada = 4.77 metros.

El teorema de Pitágoras nos permite realizar el cálculo de superficies más complejas.

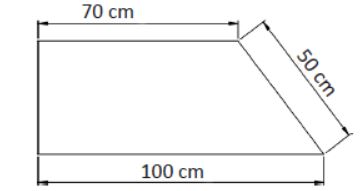
        Ejemplo aplicación teorema de Pitágoras

Para ello debemos dividir la superficie a calcular en elementos conocidos. En la siguiente figura podemos ver cómo podemos dividir la superficie en un rectángulo y un triángulo rectángulo.

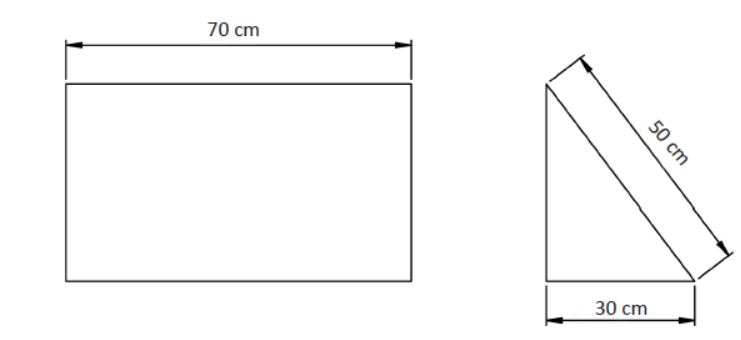
           División de la superficie en elementos conocidos

Calculamos de forma independiente tanto el área del rectángulo como el área del triángulo. Con los datos proporcionados no podremos calcular directamente ninguna de las dos superficies, pero, fijándonos en el triángulo, vemos que es un triángulo rectángulo al cual se le puede aplicar el teorema de Pitágoras.

a² = b² + c²

50² = b² + 30²

De esta forma va a ser calculada la altura del triángulo, que coincide con la del rectángulo. Es en este momento cuando podemos calcular ambas superficies.

S _rectángulo = 40 · 70 = 2800 cm²

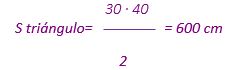
La superficie total se calcula como la suma de la superficie de los elementos independientes:

S _total = S _rectángulo + S _triángulo = 2800 + 600 = 3400 cm² 

1.4. Ángulos

Cuando se tienen triángulos, es importante conocer los ángulos que los componen. La suma de todos los ángulos de un triángulo es siempre 180°. Cuando tenemos un triángulo rectángulo, es importante conocer una serie de parámetros trigonométricos. Teniendo un triángulo rectángulo como el de la siguiente figura, vamos a definir el seno, el coseno y la tangente.

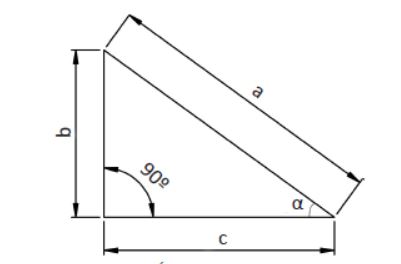
Seno de un ángulo:   senα= ^b/_a (B dividido entre a)

Coseno de un ángulo: cosα= ^c/_a (C dividido entre a)

Tangente de un ángulo: tgα= ^senα/ _cosα= ^b/_c (seno dividido entre coseno igual b dividico entre c)

Gracias a estas relaciones trigonométricas y conociendo los tres lados de un triángulo rectángulo se pueden calcular todos los ángulos. Pasamos a ver un ejemplo práctico, a la vista de los datos de la figura siguiente,

se desean conocer todos los ángulos del triángulo:

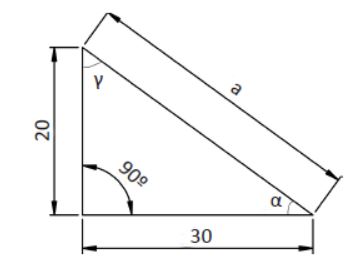
                           Datos del problema

tgα= ^b/_c= ²⁰/₃₀=0.67

α=tg^-1(0.61)=33.7º

Sabiendo que la suma de todos los ángulos del triángulo debe ser 180°, podemos calcular el último ángulo.

360 = 90 + 33.7 + γ

γ = 360 – 90 – 33.7 = 56.3º

Con estas relaciones trigonométricas también podemos calcular el valor del lado no conocido sin tener que aplicar el teorema de Pitágoras.

 senα= ^b/_a 

sen33.7= ²⁰/_a

α = 20/_sen33.7=36

PUNTO 2. UNIDADES DE MEDIDA

En fontanería, las principales magnitudes con las que se trabaja son la masa, la longitud, la superficie y el volumen. Para definir las unidades de estas magnitudes se utiliza el sistema métrico decimal. Este es un sistema de unidades único que se utiliza en todo el mundo, y así se facilita la utilización de diferentes fórmulas científicas en todos los países. En la siguiente tabla podemos observar la relación entre la magnitud y su unidad básica.

2.1. Unidades de masa

En el sistema internacional la masa se mide en gramos. Sin embargo, en ocasiones podemos tener masas muy pequeñas o muy grandes, por lo que es importante conocer otras unidades.

• Gramo (gr). Es la unidad básica de la medida de la masa.
• Decagramo (dag). Unida equivalente a 10 gramos.
• Hectogramo (hg). Unidad equivalente a 100 gramos.
• Kilogramo (kg). Unidad equivalente a 1000 gramos.
• Tonelada (Tg). Unidad equivalente a 10⁶ gramos.
• Decigramos (dg). Unidad equivalente a 10^-1 gramos.
• Centigramos (cg). Unidad equivalente a 10^-2 gramos.
• Miligramos (mg). Unidad equivalente a 10^-3 gramos.

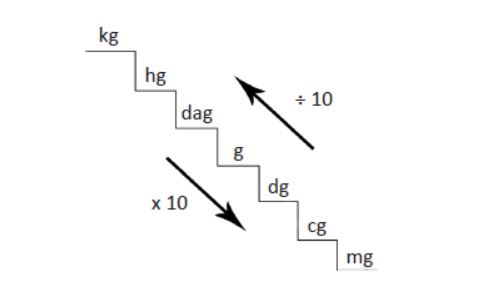
           Cambio de unidades de masa

Sí se desea pasar de una unidad inferior a una superior deberemos dividir entre diez, mientras que si se desea pasar de una unidad superior a una inferior deberemos multiplicar por diez. Por ejemplo, imaginemos que tenemos cien gramos y deseamos pasar este dato tanto a kilogramos como a centigramos:

Dato: 100 gr.

100 gr= 13^-3 kg/1gr=0.1Kg

100 gr= 100 cg/ 1gr= 10⁴ cg

Existen países, como reino unido, que no utilizan el sistema internacional, por lo que es conveniente saber cómo cambiar este tipo de unidades al sistema internacional. En este país en particular se utilizan las libras como unidad de medida de la masa. La relación entre la libra y los kg es:

1 kg = 2.205 libras

2.2. Unidades de longitud

A la vista de la tabla anterior, vemos que la unidad básica de longitud es el metro. A continuación damos la relación entre el metro y sus unidades superiores e inferiores.

• Metro (m). Es la unidad básica de la medida de la longitud.
• Decámetro (dam). Unida equivalente a 10 metros.
• Hectómetro (hm). Unidad equivalente a 100 metros.
• Kilómetro (km). Unidad equivalente a 1000 metros.
• Decímetro (dm). Unidad equivalente a 10^-1 metros.
• Centímetro (cm). Unidad equivalente a 10^-2 metros.
• Milímetro (mm). Unidad equivalente a 10^-3 metros.

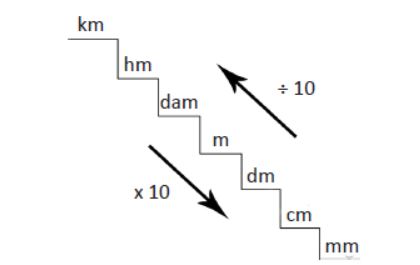
               Cambio de unidades de longitud

Vemos en la imagen que, igual que pasaban el caso de la masa, al pasar a una unidad superior se divide entre diez y al pasar a una unidad inferior se multiplica por diez. También existen unidades de medida de longitud que no se encuentran en el sistema internacional y se deben conocer. Estas unidades son las millas y los pies. La relación entre estas unidades y las unidades del sistema internacional son las siguientes:

1 milla = 1609.4 metros

1 pie = 0.707 metros

1 pulgada = 2.54 centímetros

2.3. Unidades de temperatura

Es importante conocer las diferentes unidades de la temperatura para la fontanería. En el sistema internacional la temperatura se mide en kelvin, pero existen otros tipos de unidades como son el grado Celsius y el grado Fahrenheit. Las relaciones entre las diferentes unidades de temperatura son:

• Paso de Fahrenheit a Celsius: C= 5 x(F-32) / 9
• Paso de Celsius a Fahrenheit: F= 9xC/5 + 32
• Paso de Celsius a Fahrenheit: C= K -273

Por ejemplo, imaginemos que tenemos una temperatura de 25° y queremos pasarla tanto a kelvin como a Fahrenheit:

K = 25 + 273 = 298 K

F= 9×25/5 +32= 77F

2.4. Unidades de superficie

A la vista de las ecuaciones utilizadas en apartados anteriores para el cálculo de las superficies, podemos observar que las unidades de estas son el cuadrado de las unidades de longitud. De esta forma la unidad básica en la medida de superficies es el metro cuadrado.

• Metro cuadrado (m2). Es la unidad básica de la medida de la superficie.
• Decámetro cuadrado (dam2). Unida equivalente a 100 metros cuadrados.
• Hectómetro cuadrado (hm2). Unidad equivalente a 10⁴ metros cuadrados.
• Kilómetro cuadrado (km2). Unidad equivalente a 10⁶ metros cuadrados. Decímetro cuadrado (dm2). Unidad equivalente a 10-2 metros cuadrados.
• Centímetro cuadrado (cm2). Unidad equivalente a 10^-4 metros cuadrados.
• Milímetro cuadrado (mm2). Unidad equivalente a 10^-6 metros cuadrados.

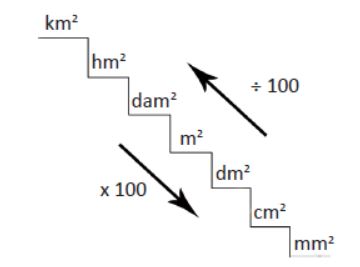
   Cambio de unidades de superficie

A diferencia de los casos anteriores, cuando queremos cambiar en unidad a una inferior deberemos multiplicar por cien, mientras que si deseamos cambiar a una unidad superior deberemos dividir entre cien. Cada escalón que subamos o bajemos se multiplicará o dividirá por cien. Por ejemplo, imaginemos que tenemos 800 m² y deseamos pasarlo tanto a hm² como a mm². La forma de operar será la siguiente:

Dato: 800 m².

800 m² x 1hm²/10⁴m² =0.08 hm²

800m² x 10⁶ mm²/1m²=8×10⁸mm²

2.5. Unidades de volumen

Las unidades del volumen son las que pueden dar a lugar a confusión. Esto es debido a que hay dos líneas de unidades para medir el volumen. La primera de ellas es la que nos marca el sistema internacional, donde la unidad básica es el metro cúbico. En esta, cada vez que se quiere calcular una unidad superior se debe dividir entre mil, mientras que si se desea calcular una unidad inferior deberemos multiplicar por mil.

• Metro cúbico (m³). Es la unidad básica de la medida del volumen.
• Decámetro cúbico (dam³⁾. Unida equivalente a 10³ metros cúbicos.
• Hectómetro cúbico (hm³). Unidad equivalente a 10⁶ metros cúbicos.
• Kilómetro cúbico (km³). Unidad equivalente a 10⁹ metros cúbicos.
• Decímetro cúbico (dm³). Unidad equivalente a 10^-3 metros cúbicos.
• Centímetro cúbico (cm³). Unidad equivalente a 10^-6 metros cúbicos.
• Milímetro cúbico (mm³). Unidad equivalente a 10^-9 metros cúbicos.

La otra es la que toma como unidad básica de unidades de volumen el litro. En este caso, el paso a unidades tanto superiores o inferiores es similar a lo explicados anteriormente para la masa o a las unidades de longitud, es decir, para calcular una unidad superior deberemos dividir entre diez, mientras que para calcular una unidad inferior se multiplica por diez.

• Litro (l). es la unidad básica del volumen.
• Decalitro (dal). unida equivalente a 10 litros.
• Hectólitro (hl). unidad equivalente a 100 litros.
• Kilolitro (kl). unidad equivalente a 1000 litros.
• Decilitro (dl). unidad equivalente a 10^-1 litros.
• Centilitro (cl). unidad equivalente a 10^-2 litros.
• Mililitro (ml). unidad equivalente a 10^-3 litros.

Existe una relación entre ambas unidades, y es que un litro equivale a un dm³.

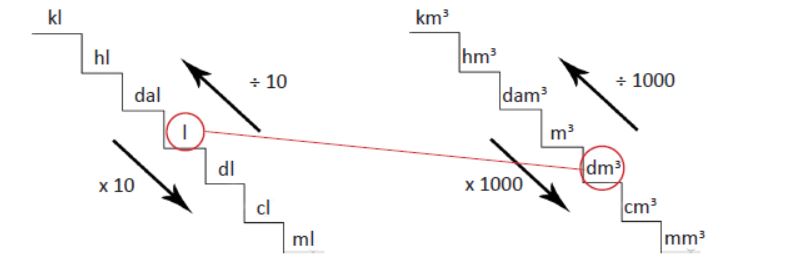
Cambio de unidades de volumen

Es necesario conocer cuáles son las unidades del volumen que no pertenecen al sistema internacional. El principal de ellos es el galón y la relación con el litro es la siguiente:

1 galón= 4.56 litros

Vamos a ver un ejemplo práctico del cambio de unidades de volumen. Imaginemos que tenemos 300 litros y queremos dar el resultado en milímetros cúbicos y en galones.

300 litros x 1dm³/1litro x 10⁶ mm3/1dm³=3 x 10⁸ mm³

300 litros x 1 galón/ 4.56 litros= 67.79 galones

PUNTO 3. DINÁMICA DE FLUIDOS

La dinámica de fluidos es la disciplina que estudia el movimiento de los líquidos. Es imprescindible para el profesional de la fontanería conocer cómo se mueven los líquidos a través de las tuberías y superficies. El estudio del movimiento de un líquido puede llegar a ser muy complicado, para ello debemos tomar una serie de consideraciones. Un fluido ideal tiene las siguientes características:

• No deberemos tener en cuenta los posibles rozamientos entre las partes internas de un fluido. Esto es considerar el fluido como no viscoso.
• Se considera la densidad del fluido constante en el tiempo. Esto es considerar que el flujo es estacionario.
• La densidad del fluido será constante en el tiempo. Esto equivale a decir que el fluido sea incompresible.
• El momento angular del fluido debe ser nulo, por lo que no se producirán torbellinos. De esta forma se consideran flujo irrotacional.

3.1. Ecuación de continuidad

La ecuación de continuidad nos da el cambio de velocidad que se produce en el fluido cuando varía la sección de la tubería. Esto es:

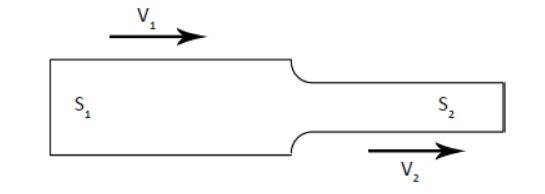
                  Esquema reducción en tubería

                            v₁ x S₁= v₂ x S₂

Donde:

• S representa las secciones de las dos partes de la tubería.
• v son las velocidades en cada uno de los tramos.

Pasamos a ver un eje del acta de la ecuación concluida. Tenemos una tubería con una pequeña tobera que disminuye la sección de esta. El radio de la primera parte de la tubería es de 20 mm y la velocidad del líquido al pasar por ella es de 5 m/s. Si deseamos que la velocidad de salida sea de 10 m/s se debe calcular el radio de la sección de salida. Calculamos el valor de la primera sección a partir de su radio:

S₁ = π · r² = π · 20² = 1256.6 mm² = 0.001256 m²

Ahora podemos aplicar la ecuación de continuidad con la que calcularemos el valor de la segunda sección:

v₁ · S₁ = v₂ · S₂

5 · 0.1256 = 10 · S₂

s₂= 5x 0.001256/10= 6.3 x 10^-4 m²=628 mm²

Con esta sección podemos calcular el valor del radio:

3.2. Principio de Bernoulli

El principio de Bernoulli señala que el comportamiento de un fluido que circula a través de una tubería será siempre constante. Gracias a este principio, sí consideramos una tubería, sabemos que la suma de las energías del primer tramo será igual a la suma de las energías del segundo. En la circulación de un fluido se deben considerar tres tipos de energías diferentes:

• Energía de presión. Es la energía que tiene un fluido a causa de la presión.
• Energía cinética. Energía de un fluido por el hecho de tener velocidad.

                            E_c= v² x ρ / 2

• Energía potencial. Energía del fluido debido a que se encuentra a cierta altura.

                           E_p= ρ x g x h

Donde:

• v. Es la velocidad del fluido.
• P. Es la presión.
• ρ. Es la densidad del fluido.
• h. Es la altura a la que se encuentra la tubería.
• g. Es el valor de la gravedad que corresponde a 9.81 m/s2.

La ecuación de Bernoulli es:

P₁ + Ec₁ + Ep₁= P₂ + Ec₂ + Ep₂

P1 + V²₁ x ρ/ 2 + ρ x g x h₁₌  P₂ + v²₂ x ρ/2 + ρ x g x h₂

Consideremos que el ejemplo de la figura inferior es una tubería por la que circula agua. A la vista de los datos se desea calcular la velocidad de salida: Densidad del agua = 1 kg/litro.

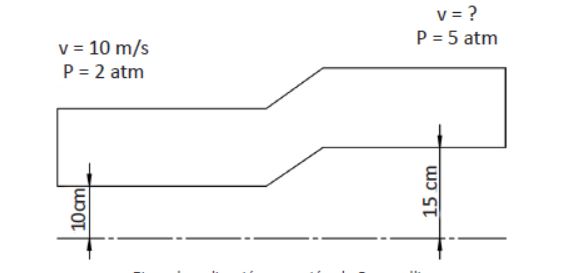
                 Ejemplo aplicación ecuación de Bernoulli

Aplicamos directamente la ecuación de Bernoulli:

P1 + V²₁ x ρ/ 2 + ρ x g x h₁₌  P₂ + v²₂ x ρ/2 + ρ x g x h₂

2 + 102 x1 /2 + 1 x 9.81 x 0.1 = 5 + v²₂ x 1/2 + 1 x 9.81 x 0.15

2 + 50 + 0.981= 5 + v²₂ x 1/2 + 1.47

 v₂= 10.14 m/s

3.3. Efecto Venturi

El efecto Venturi es aquel donde un fluido que se encuentra en movimiento dentro de una tubería, si se disminuye la presión, su velocidad aumentará al pasar de una sección mayor a una menor. En este caso podemos aplicar la ecuación de Bernoulli teniendo en cuenta que no existirá diferencia de altura, pero sí una diferencia en la sección de la tubería.

P¹ + V²₁ x ρ / 2= P₂ + v²₂ x ρ/2

De esta forma podemos calcular la velocidad de salida del fluido como:

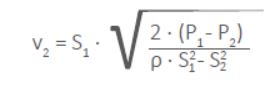
Imaginemos como ejemplo la tubería de la figura siguiente. Con los datos que se tienen, y sabiendo que el líquido es agua, deseamos calcular la velocidad de salida.

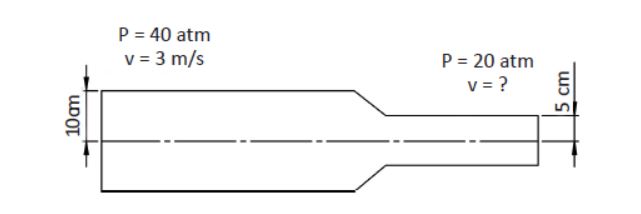
Ejemplo de cálculo de efecto Venturi

S₁ = π · r² = π · 0.1² = 0.0314 mm²

S₂ = π · r² = π · 0.05^{2 =} 0.00785 mm²

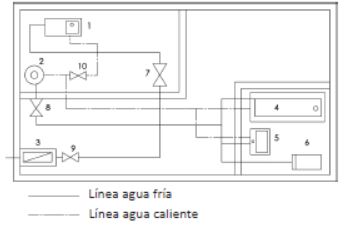
PUNTO 4. INTERPRETACIÓN DE PLANOS Y SIMBOLOGÍA

Es esencial que el profesional de la fontanería tenga la capacidad de interpretar unos planos dados. Para ello lo primero que se debe conocer es la simbología específica de esta rama. Los principales símbolos utilizados en la fontanería son los siguientes:

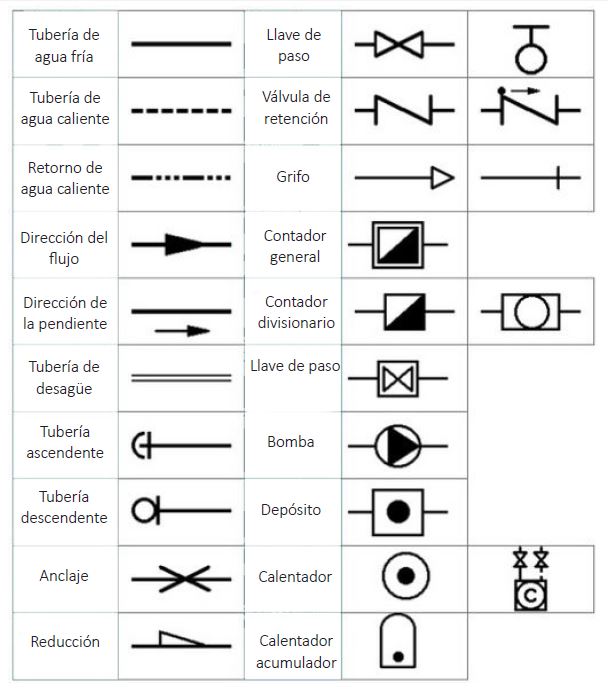
                                    Principales símbolos

Los símbolos expuestos anteriormente son los correspondientes a las tuberías, pero existen gran número de símbolos que el profesional de la fontanería debe reconocer y que hacen referencia a otros elementos. En las siguientes tablas se muestra toda la simbología que es necesario que el profesional conozca.

                          

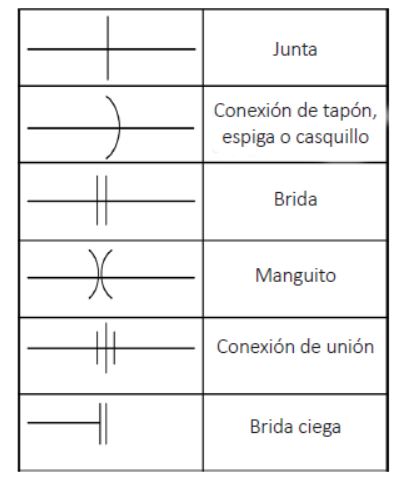
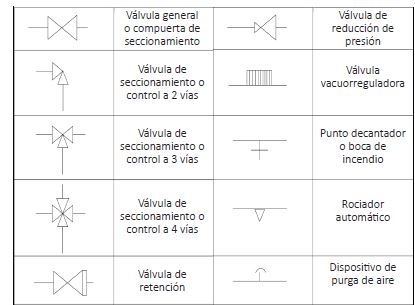
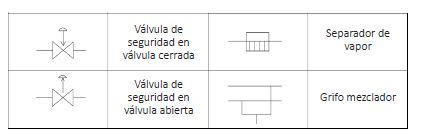
                 Simbología de juntas                                                                                                                                                 Simbología de válvulas

 

   

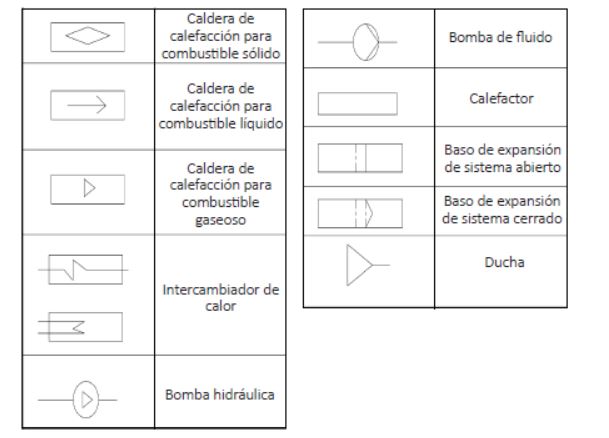
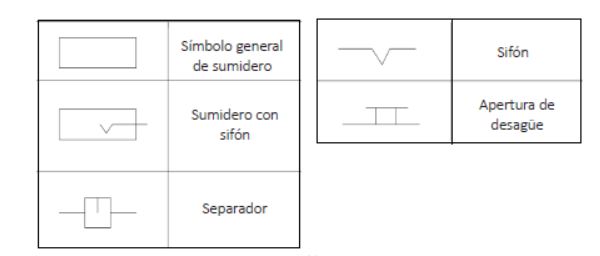
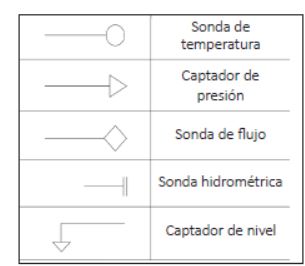
                                      Equipamientos                                                                                                       Sumideros                                                                                           Sondas y captadores

 

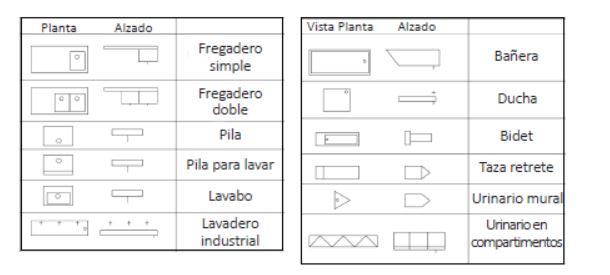
                                            Aparatos sanitarios

Conociendo toda esta simbología típica de la fontanería, podremos localizar en un plano los diferentes elementos de interés. La siguiente imagen representa el plano unifilar típico de fontanería de una vivienda: